HyperLogLog in Presto: A significantly faster way to handle cardinality estimation
대규모 데이터 집합에서 고유 요소의 수를 계산하는 작업은 필요하지만, 계산 집약적이다. 예를 들어 한 주 동안 Facebook을 방문한 고유 사용자 수를 확인해야 한다 할 때, 기존 SQL 쿼리로 이 작업을 수행하려면 며칠의 시간과 테라바이트의 메모리가 소요된다. HyperLogLog(HLL)은 APPROX_DISTINCT라는 함수를 사용해 고유 요소의 대략적 추정 개수를 제공하는 방식으로 동작한다. HLL을 사용하면 1MB 미만의 메모리로 12시간 안에 동일한 계산을 수행할 수 있다.
What led to HyperLogLog?
중복 항목이 포함된 카디널리티 n 인 대규모 데이터 집합이 있고 여기서 고유 요소 수를 구하려고 가정하자. 요소를 정렬하거나 단순한 고유 요소 집합을 유지하는 일반적 접근 방식은 계산 집약적이거나, 너무 많은 메모리를 요구하기 때문에 비실용적이다. 복잡성이 증가하는 순서대로 알고리즘을 살펴보고 HLL의 동작 방식을 이해해보자.
A simple estimator
답을 찾기 위해서는 추정치를 출력하는 알고리즘이 필요하다. 이 추정치는 오차가 있을 수 있지만 합리적인 오차 범위 내에 존재해야 한다. 먼저 아래와 같이 반복되는 가상의 데이터 집합을 생성한다.
- 0와 1 사이에 균등 분포를 이루는 n개의 숫자를 생성한다.
- 숫자 중 일부를 임의의 횟수 만큼 임의로 복제한다.
- 위의 데이터 집합을 임의의 방식으로 섞는다.
항목이 균등하게 분포되어 있으므로 집합의 최소값 ()을 구하고 고유 항목의 수를 으로 추정할 수 있다. 그러나 항목을 균등하게 분산하기 위해 해시 함수를 사용하고 항목 자체 대신 해시된 값으로 카디널리티를 추정할 수 있다. 아래는 해시 값이 정규화되어 0과 1 사이에 균일하게 분포된 간단한 예이다.
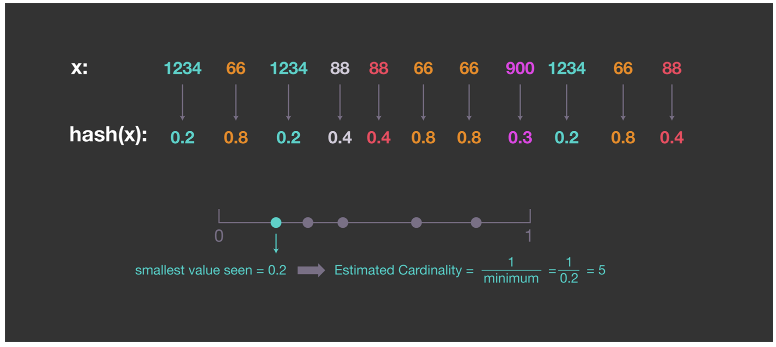
이 절차는 간단하지만 최소 해시값에 의존하기 때문에 편차가 크고, 이 값이 너무 작을 경우 추정치가 부풀려질 수 있다.
Probabilistic counting
이전 방법의 높은 변동성을 줄이기 위해 해시값의 시작 부분에서 0비트 수를 세는 개선된 패턴을 사용할 수 있다. 이 패턴은 주어진 해시(x)가 최소 i개의 0으로 끝날 확률이 이기 때문에 작동한다. 아래 그림은 세 개의 연속된 0이 관촬될 확률을 보여주는 예이다.
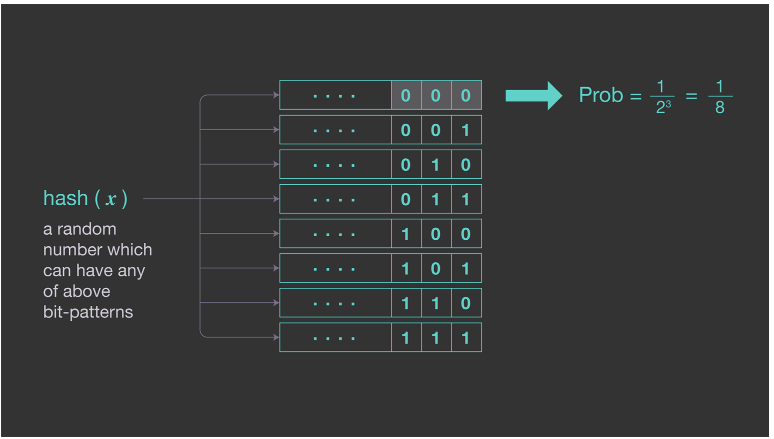
평균적으로 k개의 연속 0 시퀀스가 2^k개의 고유 항목 마다 한 번씩 발생한다. 이 패턴을 사용하여 고유한 요소의 수를 추정하려면 가장 긴 연속 0 시퀀스의 길이를 기록하기만 하면 된다. 수학적으로 를 의 연속 0의 수로 나타낸다면 카디널리티 집합 은 이며 R은 이 된다. 이 방법은 두 가지 단점이 있다.
- 의 식 때문에 카디널리티는 2의 계수 만큼의 추정치밖에 제공하지 못한다.
- 추정치의 변동성은 여전히 높다. 최대 를 기록하기 때문에 해시 값이 너무 많은 연속적인 0을 가진 항목 하나만 있으면 카디널리티에 대한 매우 부정확한(과대한) 추정치를 생성할 수 도 있다.
장점은 추정기의 메모리 사용량이 매우 적다는 점이다. 보이는 연속된 0의 최대 개수만 기록하기 때문에 32비트까지의 선행 0의 시퀀스를 기록하려면 추정기는 5비트의 메모리만 있으면 된다.
Improving accuracy: LogLog
추정치를 개선하기 위해 하나 대신 여러 개의 추정치를 저장하고 결과를 평균화할 수 있다. 단일 추정기의 분산은 여러 개의 독립 추정기를 사용하고 결과를 평균화함으로써 감소한다.
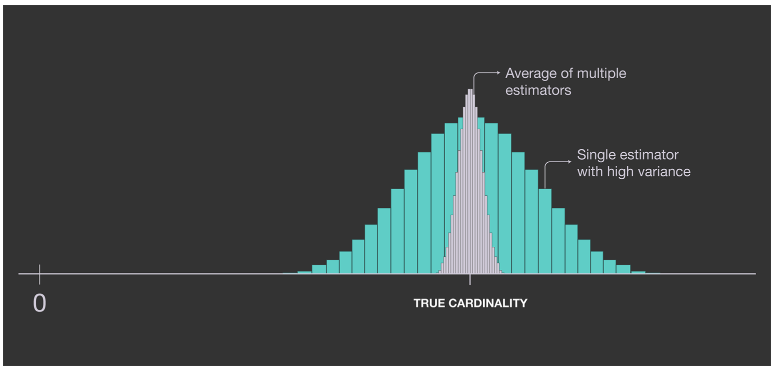
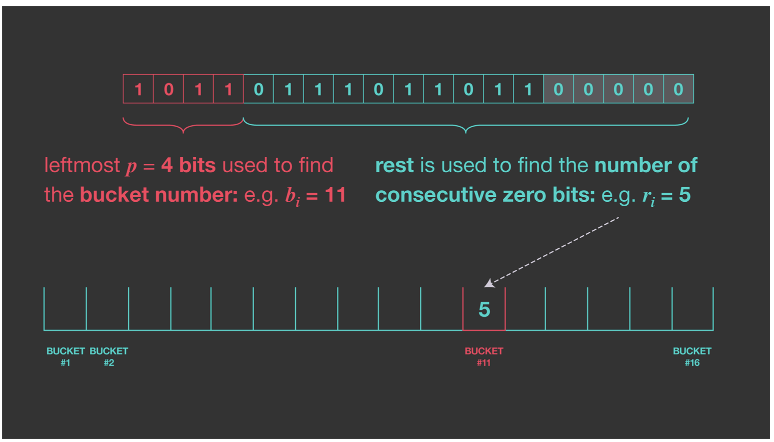
m개의 독립 함수 를 사용해 이를 달성할 수 있다. 각각의 최대 연속 0 수를 얻으면 () 추정치 은 이 된다. 그러나 이를 위해 각 입력 가 여러 독립 해시 함수를 통과해야 하므로 계산 비용이 크다. Durand와 Flajolet이 제안한 해결 방법은 단일 해시 함수를 사용하지만 출력의 일부를 사용해 값을 여러 버킷 중 하나로 분할하는 방법이다. 입력 항목을 m 버킷으로 나누기 위해 해시 값의 처음 몇 k 비트를 버킷에 인덱스로 사용하고 남은 부분에서 가장 긴 연속 0 시퀀스를 계산하는 방법을 제안한다.
예를 들어 hash(input)=101101101101100000일때 가장 왼쪽 4개(k = 4)의 비트를 사용해 버킷 인덱스를 찾는다. 그리고 나머지 오른쪽 비트에서 연속 0의 개수를 얻을 수 있다. 따라서 이 예에서는 버킷 11에 값을 5로 업데이트 할 수 있다.
버킷이 여러개 라는 것은 기본적으로 서로 다른 해시 함수가 있는 상황을 시뮬레이션 하는 것이다. 이렇게 하면 정확도 측면에서는 비용이 들지 않으며 많은 독립적인 해시 함수를 계산할 필요도 없어진다. 이 절차를 확률적 평균화라 한다. 마지막으로 아래 수식을 사용해 m개의 버킷 값을 사용해 고유 값의 개수를 추정한다.
통계 분석에 따르면 위 추정치는 더 큰 추정치에 대한 예측 가능한 편향이 있는 것으로 나타났다. Durand-Flajolet는 이 편향을 보정하기 위해 상수 0.79402를 도출했다.(LogLog 알고리즘) 버킷 수가 m인 경우 추정기의 표준 오차는 으로 줄어든다. 따라서 각 버킷이 5비트인 2048개의 버킷을 사용하면 평균 오차는 약 2.8%이며 버킷당 5비트는 원본 논문에 따라 의 카디널리티를 추정하기에 충분하고 2048 * 5 = 1.2KB의 메모리만 필요로 한다. 이는 기본적으로 1KB의 메모리로 꽤 좋은 결과이다.
HLL: Improving accuracy even further
두 가지를 추가로 개선하면 더 나은 결과를 얻을 수 있다.
Durand-Flajolet은 특이값이 이 추정기의 정확도를 크게 떨어트린다는 점을 발견했다. 따라서 평균을 내기 전에 가장 큰 값을 버리면 정확도를 향상시킬 수 있다. 구체적으로, 최종 추정치를 생성하기 위해 버킷 값을 수집할 때 가장 작은 70%의 값만 유지하고 나머지는 평균을 내기 위해 버리면 정확도를 에서 로 개선할 수 있다.(SuperLogLog 알고리즘)
HLL은 평가 함수에서 다른 유형의 평균을 사용한다. LogLog에서 사용되는 기하 평균 대신 조화 평균을 사용해 필요한 저장공간을 늘리지 않고도 오차를 미만으로 약간 낮출 것을 제안했다. 이 모든 것을 종합하면 고유값의 개수에 대한 HLL 추정치를 구할 수 있다.
HLL 집합에 대한 연산
집합 병합 연산은 HLL에서 간단하게 계산할 수 있으며 무손실이다. 두 개의 HLL 데이터 구조를 결합하려면 두 데이터 구조의 해당 버킷 값의 최대값을 취한 다음 이를 결합된 HLL의 해당 버킷에 할당하기만 하면 된다. 이는 두 데이터 집합을 처음부터 하나의 HLL에 제공한것과 똑같다. 이런 간단한 집합 병합 연산을 통해 동일한 해시 함수와 동일한 수의 버킷을 사용해 여러 머신에서 독립적으로 작업을 쉽게 병렬화할 수 있다.