2647. Color the Triangle Red

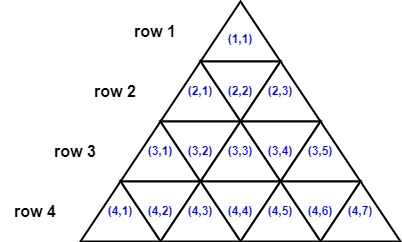
You are given an integer n. Consider an equilateral triangle of side length n, broken up into n2 unit equilateral triangles. The triangle has n ith row has 2i - 1 unit equilateral triangles.

The triangles in the ith``(i, 1) to (i, 2i - 1). The following image shows a triangle of side length 4 with the indexing of its triangle.

Two triangles are neighbors if they share a side. For example:

• Triangles (1,1) and (2,2) are neighbors
• Triangles (3,2) and (3,3) are neighbors.
• Triangles (2,2) and (3,3) are not neighbors because they do not share any side.

>k

1. • If there is no such triangle, stop the algorithm.
2. Color that triangle red.
3. Go to step 1.

Choose the minimum k possible and set k triangles red before running this algorithm such that after the algorithm stops, all unit triangles are colored red.

Return a 2D list of the coordinates of the triangles that you will color red initially. The answer has to be of the smallest size possible. If there are multiple valid solutions, return any.

class Solution {
public:
    vector<vector<int>> colorRed(int n) {
        vector<vector<int>> res;
        for(int i = n; i >= 1; i--) {
            int d = (n - i) % 4;
            if(d == 0) for(int j = 2 * i - 1; j > 0; j -= 2) res.push_back({i,j});
            else if(d == 1) {
                if(2 <= i) res.push_back({i,2});
            } else if(d == 2) for(int j = 2 * i - 1; j > 2; j -= 2) res.push_back({i,j});
            else res.push_back({i,1});
            if(i == 1 and 1 <= d and d <= 2) res.push_back({1,1});
        }
        return res;
    }
};