BST
Binary Search Tree란 각각의 노드가 최대 두 개의 자식 노드를 가지는 트리 자료구조이다
최악의 케이스의 경우 O(n)을 가진다
평균으로 O(log n)을 가진다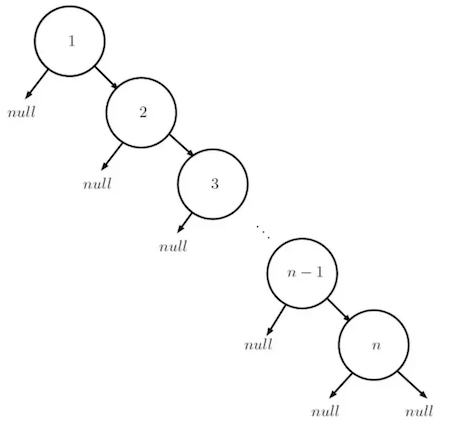
Big-O Notation
| Algorithm | Average | Worst case |
|---|---|---|
| Space | O(n) | O(n) |
| Search | O(log n) | O(n) |
| Insert | O(log n) | O(n) |
| Delete | O(log n) | O(n) |
BST 예시
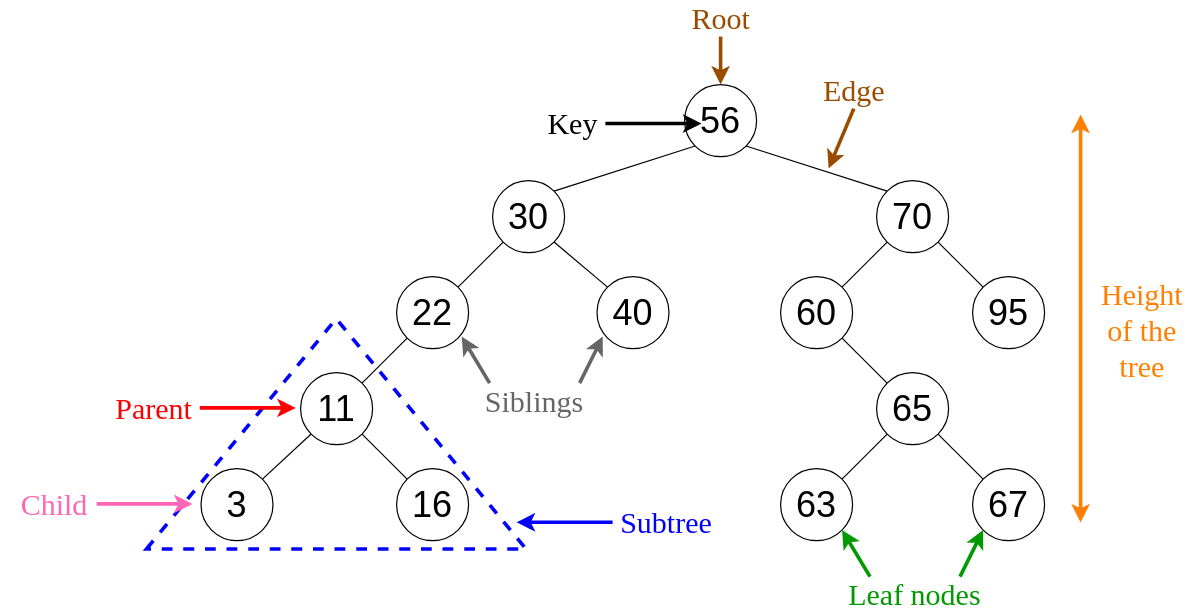
Root
최상위 노드
Key
노드에 삽입된 Value
Edge
노드간 연결하는 간선
Leaf Node
자식노드가 존재하지 않는 최하위 노드
Sibilings
한 부모노드가 가지는 두개의 자식노드의 관계
Parent
노드 11이 노드 3을 가리킬 때 노드 11을 노드 3의 부모노드라 한다
Child
노드 3이 노드 11에게 가리켜질 때 노드 3을 노드 11의 자식노드라 한다
Sub Tree
전체 트리구조에서 부차적으로 가지는 트리구조
부트리라고 한다
Height
루트노드에서 최하위 리프노드까지의 단계의 수를 높이라 한다
Level
루트노드는 레벨 0이다
루트노드부터 한단계씩 밑으로 내려갈수록 레벨이 1씩 증가한다
BST Order(이진트리 순회)
Preorder(전위순회)
- 노드를 방문한다
- 왼쪽 서브트리를 전위순회 한다
- 오른쪽 서브트리를 전위순회 한다
56 -> 30 -> 22 -> 11 -> 3 -> 16 -> 40 -> 70 -> 60 -> 65 -> 63 -> 67 -> 95
Inorder(중위순회)
- 왼쪽 서브트리를 중위순회 한다
- 노드를 방문한다
- 오른쪽 서브트리를 중위순회 한다
3 -> 11 -> 16 -> 22 -> 30 -> 40 -> 56 -> 63 -> 65 -> 67 -> 60 -> 70 -> 95
Postorder(후위순회)
- 왼쪽 서브트리를 후위순회 한다
- 오른쪽 서브트리를 후위순회 한다
- 노드를 방문한다
3 -> 16 -> 11 -> 22 -> 40 -> 30 -> 63 -> 67 -> 65 -> 60 -> 95 -> 70 -> 56